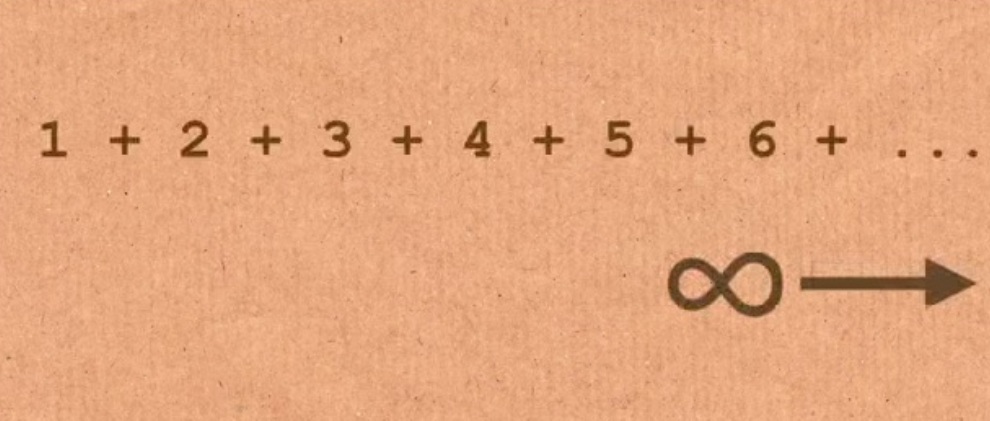Έχετε προσπαθήσει να προσθέτετε κάθε αριθμό από το ένα στο άπειρο; Αναρωτιέστε ποιο είναι το άθροισμα;
Προφανώς, εάν σταματήσετε αυτή τη σειρά σε οποιοδήποτε σημείο πριν από το άπειρο, θα έχετε έναν απίστευτα τεράστιο αριθμό.
Αλλά στην πραγματικότητα, αν υπολογίσετε την άπειρη σειρά ως σύνολο, θα πάρετε μια ασυνήθιστα συγκεκριμένη, μη απεριόριστη απάντηση: -1/12.
Πώς γίνεται αυτό;
Πρώτον, θα πρέπει να καθορίσουμε ορισμένους μαθηματικούς όρους.
Μιλάμε για φυσικούς αριθμούς, οι οποίοι είναι θετικοί ακέραιοι αριθμοί. Εάν συμπεριλάβετε κλάσματα η δεκαδικούς αριθμούς θα έχετε διαφορετικά αποτελέσματα.
Δεύτερον, η σειρά αυτή είναι γνωστή ως αποκλίνουσα, επειδή οι όροι της συνεχίζουν να αυξάνονται χωρίς περιορισμό. Είναι απλή πρόσθεση, αλλά αντί να προσθέτουμε μεμονωμένους αριθμούς, δεδομένου ότι θα χρειαζόταν… άπειρο χρονικό διάστημα, προσθέτουμε σύνολα αριθμών.
Οι μεταβλητές ιδιότητες, που θυμούνται όσοι ήταν καλοί στην άλγεβρα, ισχύουν για όλα για σύνολα, αλλά τα σύνολα έχουν πρόσθετες ιδιότητες που οι αριθμοί δεν τις απολαμβάνουν. Αυτές οι ιδιότητες καθιστούν δυνατή την παρεκβολή των συνόλων άπειρων σειρών σε φυσικούς αριθμούς.
Αυτοί οι φυσικοί αριθμοί δεν είναι προσεγγίσεις του αθροίσματος της άπειρης σειράς αλλά του μέσου όρου όλων των όρων της σειράς.
Με μια πρώτη ματιά, αυτό μπορεί να μοιάζει με εξαπάτηση, αλλά δεν είναι!
Το πιο σημαντικό πράγμα που πρέπει να συνειδητοποιήσουμε για τα ποσά των άπειρων σειρών είναι ότι αντιστοιχούν στην πραγματικότητα, ακόμη και αν δεν συμμετέχουν κατ ‘ανάγκην στην πραγματικότητα.
Στην πραγματικότητα, όλοι οι αριθμοί, τα σύνολα και οι μαθηματικές αρχές είναι απλώς αφηρημένες έννοιες. Αυτό θα πρέπει να κάνει το γεγονός ότι το άθροισμα όλων των φυσικών αριθμών είναι -1/12 πολύ πιο εύκολο να γίνει αντιληπτό στο μυαλό μας, αφού δεν μπορούμε να πάρουμε μια αριθμομηχανή και να προσθέτουμε κάθε αριθμό για πάντα, αλλά μπορούμε να περιγράψουμε ένα σύστημα που κάνει ακριβώς αυτό.
Ούτε οι αριθμοί ούτε τα άπειρα σύνολα προκύπτουν από μόνα τους. Δεν υπάρχει φυσικό πράγμα που να αντιστοιχεί στον αριθμό -1/12, ακριβώς όπως δεν υπάρχει φυσικό πράγμα που να αντιστοιχεί στο άθροισμα όλων των φυσικών αριθμών.
Αλλά όταν αυτές οι έννοιες παράγουν δοκιμαστέα, παρατηρήσιμα αποτελέσματα σε φυσικά πειράματα, γίνονται μέρος της μαθηματικής πραγματικότητας. Αυτό είναι που κάνει καταρχάς τους αριθμούς χρήσιμους για την καταμέτρηση των πραγμάτων και την επίλυση των προβλημάτων. Αν μια εξίσωση «βγαίνει» μπορεί να περιγραφεί με ακρίβεια ως αλήθεια.
Το άθροισμα όλων των φυσικών αριθμών είναι ένα εξαιρετικό παράδειγμα επειδή οι φυσικοί το χρησιμοποιούν. Για παράδειγμα, χρησιμοποιείται από τους κβαντικούς φυσικούς για τη πυκνότητα της ενέργειας σε αυτό που ονομάζεται φαινόμενο Casimir, τη μικρή ελκτική δύναμη που δρα μεταξύ δύο αφόρτιστων αγώγιμων πλακών παράλληλων μεταξύ τους όταν βρίσκονται σε πολύ κοντινή απόσταση.
Μια δύναμη που διαπερνά ολόκληρο το σύμπαν πρέπει να είναι άπειρη – και τα πειράματα έχουν δείξει ότι η διαφορά ενέργειας μεταξύ της παρατηρούμενης δύναμης (μεταξύ των δύο πλακών) και της δύναμης που ενεργεί στο υπόλοιπο σύμπαν αντιστοιχεί στο άθροισμα όλων των φυσικών αριθμών.
Δεν αποτελεί έκπληξη το γεγονός ότι με άπειρα σύνολα είναι δύσκολο να κάνουμε υπολογισμούς. Το σύμπαν δεν παράγει στην πράξη άπειρη ενέργεια σε ένα εργαστήριο, αλλά η ποσότητα ενέργειας που παράγει το φαινόμενο Casimir είναι πάντα σύμφωνη με αυτό το άθροισμα.
Ως αποτέλεσμα, όταν οι φυσικοί και οι μαθηματικοί πρέπει να περιγράψουν την επίδραση του αποτελέσματος Casimir σε άλλα συστήματα, αντικαθιστούν το άθροισμα όλων των φυσικών αριθμών με -1/12 και εκπληκτικά επιτυγχάνουν ακριβή, παρατηρήσιμα αποτελέσματα.